 Man denkt ja immer, die Mathematik sei logisch. Dabei gilt es zu beachten, dass Logik nicht unbedingt etwas mit gesundem Menschenverstand zu tun hat. Und das ist auch gut so – niemand wollte einen nur logisch denkenden Menschen. Aber nur logisch ist die Mathematik auch nicht – und das mag vielen neu erscheinen. Sie ist wie eine kleine (oder große) Phantasiewelt, in der alles möglich ist.
Man denkt ja immer, die Mathematik sei logisch. Dabei gilt es zu beachten, dass Logik nicht unbedingt etwas mit gesundem Menschenverstand zu tun hat. Und das ist auch gut so – niemand wollte einen nur logisch denkenden Menschen. Aber nur logisch ist die Mathematik auch nicht – und das mag vielen neu erscheinen. Sie ist wie eine kleine (oder große) Phantasiewelt, in der alles möglich ist.
Hier also ein paar Exkurse ins Wunderland, mit dem ich mich gerade vertraut mache:
Ich finde es immer wieder amüsant manchen Verwandten zu erklären, dass es tatsächlich parallele Geraden gibt, die sich doch tatsächlich entgegen jeder Erwartung schneiden. Unter bestimmten Bedingungen schneiden sie sich wirklich, obwohl zumindest in der Schule parallele Geraden meistens dadurch klassifiziert werden, dass sie sich eben nicht schneiden. Oder plötzlich schneiden sich Diagonalen eines Parallelogramms auf einmal nicht mehr, die sich zumindest in der Schule immer schneiden würden.
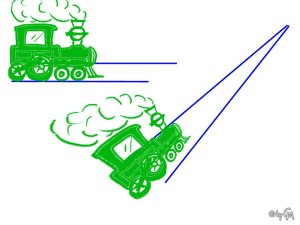
Wo schneiden sich Parallelen? Im Unendlichen bzw. mathematischer gesprochen, schneiden sich parallele Geraden immer in einer projektiven Ebene – dort haben je zwei Geraden immer! einen Schnittpunkt. Noch genauer, würde man sagen, dass sie sich auf der Ferngeraden einer projektiven Ebene schneiden. Einzusehen ist dieser projektive/im Unendlichen liegende Schnittpunkt ja eigentlich schon: Betrachtet man einmal zwei parallel verlaufende Eisenbahnschienen, die bis in den Horzont hinein immer gerade aus gehen, dann erscheint es für das Auge auch so, als ob sie sich da ganz weit hinten schneiden würden.
So etwas verwirrt vielleicht manchen Schüler, aber das sollte eigentlich kein Grund sein, es nicht auch einmal anzusprechen – im Gegenteil. Meistens verankert sich doch Merkwürdiges umso besser im Gehirn. Warum hieße es sonst wohl merk-würdig?
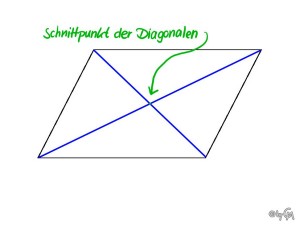
Wann sich Diagonalen eines Parallelogramms nicht schneiden, ist schon schwerer zu erklären – zumindest wenn man schon einmal davon ausgeht, dass nicht jeder weiß, was ein Parallelogramm ist. Also, ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten parallel sind – hier werden die Paralleln vorher abgeschnitten, bevor sie sich im Unendlichen schneiden können ;)
Die anderen vier Schnitttpunkte sind da interessanter. Denn die gibt es wenigstens – ganz im Gegenteil zu dem Diagonalenschnittpunkt. Zumindest kommt der unter bestimmten Bedinungen nicht vor. Beispielsweise wenn man sich in einem Körper der Charakteristik≠2 befindet – dort gibt es kein 1/2 (da hier 2=0 ist und durch Null darf man ja bekanntlich nicht teilen). Dadurch, dass es kein 1/2 gibt, können sich die Diagonalen eines Parallelogramms nicht wie gewöhnlich in der Mitte halbieren – also schneiden sie sich nicht.
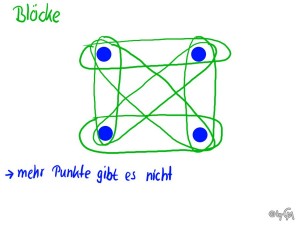
Ein anderes – meiner Meinung nach abstrakteres, aber auch anschaulicheres Beispiel wäre die kleinste affine Ebene. Diese besteht nur aus 4 Punkten und die Geraden in dieser Ebene, sehen Gerden eigentlich kaum mehr ähnlich, sondern sehen eher wie Blöcke aus.
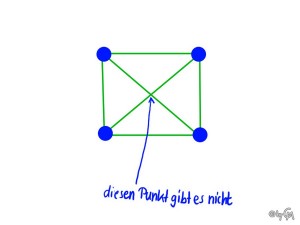
Die Gerade/Blöcke, die die Diagonalen darstellen, schneiden sich nicht in der Mitte, da die Ebene, in der sie sich befinden, wie gesagt, nur aus 4 Punkten besteht. Der Diagonalenschnittpunkt wäre der 5. Punkt und den gibt es nicht, also schneiden sie sich nicht.
Und nun noch etwas lustiges zum Schluss:
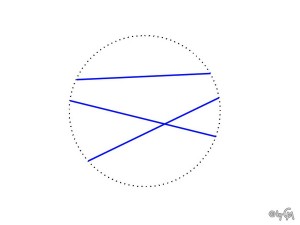
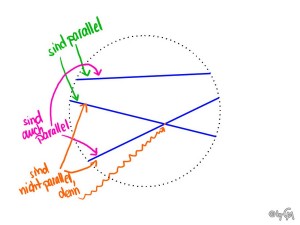
Es gibt auch Geraden, die aussehen, als würden sie sich schneiden, in Wirklichkeit aber parallel sind. Dieser Fall lässt sich in der hyperbolischen Ebenen beobachten.
Man stellt sie sich als eine Art Kreisscheibe vor, deren Rand fehlt. Die Geraden die in dieser Ebene keinen Schnittpunkt haben, sind parallel, obwohl sie sich vielleicht schneiden würden, wenn man sie über den Kreis hinaus weiter zeichen würde. Da die hyperbolische Ebene aber noch vor dem Rand des Kreises endet, schneiden sich die Geraden, die sich in dem Kreis nicht schneiden, nie.
 Nun ist es an euch zu entscheiden:
Nun ist es an euch zu entscheiden:
Ist die Mathematik eine verrückte Welt oder doch eher ein Wunderland?
Hallo Cordula,
ich will ja jetzt kein Spielverderber sein (vor allem, da ich verspätet kommentiere…), aber
parallele Geraden schneiden sich nie, auch nicht im Unendlichen ;-), es sei denn sie sind identisch.
Denn wenn wir die affine Ebene zur projektiven vervollständigen, werden aus parallelen Geraden nichtparallele…sie schneiden sich ja…
Aber sonst finde ich den Beitrag gut :-).
Viele Grüße,
Eugen
Hi Eugen,
ja, da war ich zugegebenermaßen etwas ungenau. Du hast natürlich :) Recht. Genauer müsste man sagen, dass die parallelen Geraden, die man in der affinen Ebene hat, in der projektiven Erweiterung dieser affinen Ebene – also in der projektiven Ebene – eigentlich keine parallelen Geraden mehr sind, da sie sich ja dann auf der Ferngeraden schneiden. Da diese vom Affinen aus gesehen aber unendlich weit weg scheint (die Parallelen werden sozusagen dorthin projiziert), fand ich das Vorstellungsbild von den sich im ‚Unendlichen‘ schneidenden parallelen Geraden ganz passend – wenn auch mathematisch nicht vollständig korrekt ;)
Ich freu mich aber, dass dir der Beitrag sonst gefällt :) Er ist sozusagen jetzt mit den erläuternden Kommentaren durch den Eugen-TÜV gekommen ;)
Viele Grüße,
Cordula
Ein ganz toller Beitrag zu einer verrückten Wunderwelt der Mathematik, aber wie eingangs von dir erwähnt, kannst du ja an „Verwandten“ üben, wie du es später Schülern erklären kannst.
Mit den Bildern hast du es wirklich anschaulich erklärt. Toll.
Ich habe mich entschieden: Die Mathematik ist eine verückte Wunderwelt ;)
Am Anfang ist diese Welt unübersichtlich und stellenweise sogar abschreckend. Die einzelnen Teilgebiete scheinen wie Inseln in einem weiten Meer zu sein, zwischen denen es keine Verbindung gibt. Anfangs steht man ein bisschen verloren in in dieser Welt. Je mehr man sie aber erkundet, findet man wundersame Wege von einer Insel zur anderen, die man anfangs gar nicht gesehen hatte oder für möglich hielt. Und dann gewinnt man langsam einen Blick für das große Ganze und erkennt die volle Schönheit dieser wunderbaren Welt ;)
Genug philosophiert – da hast du einen wundervoll illustrierten Beitrag geschrieben!