Ich habe mir als Schüler nie merken können, wann man denn nun die erste oder die zweite Ableitung Null setzt, um etwas über Extremwertstellen oder Wendepunkte herauszufinden, geschweige denn, was man zusätzlich noch überprüfen muss. Und seien wir doch mal ehrlich: Sich das in einer Klausur ewig zu überlegen – dafür hat man schlichtweg keine Zeit.
Deshalb wollte ich hier einmal mit euch, und vor allem mit allen, die kurz vor ihrem Abitur stehen, das kleine Merkbild teilen, das uns damals unser Mathelehrer gegeben hat. Ich verwende es heute noch, um schnell zu schauen, welche Ableitung ich für welche Überprüfung brauche:
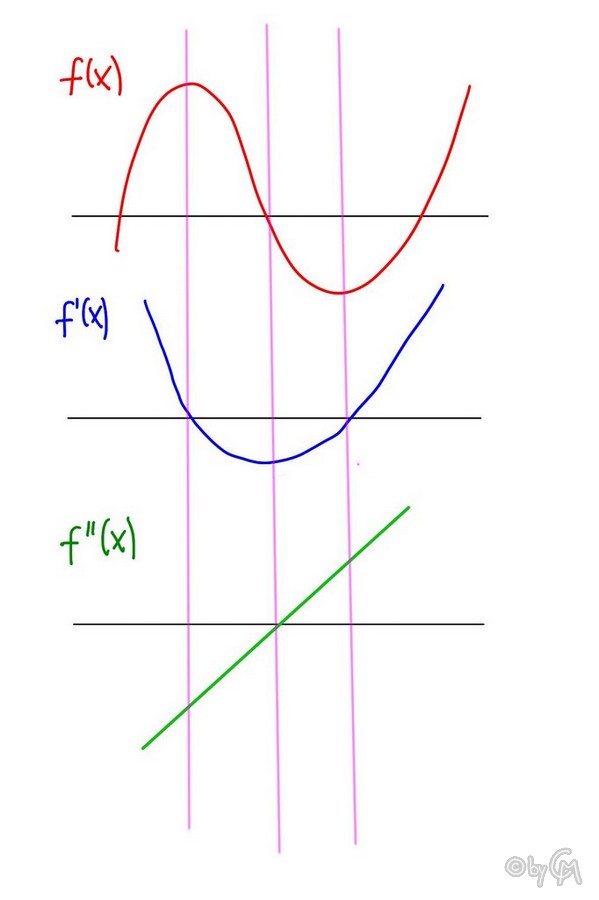 Ich denke, dass man sich anhand von diesen drei kleinen Bildchen recht schnell Folgendes klar machen kann:
Ich denke, dass man sich anhand von diesen drei kleinen Bildchen recht schnell Folgendes klar machen kann:
Extremwerte:
Notwendige Bedingung:
Hat die Funktion an der Stelle x* einen Extremwert, so ist an der Stelle x* ihre erste Ableitung gleich Null.
Hinreichende Bedingung:
Ist die zweite Ableitung an der Stelle x* kleiner als Null, also negativ – bzw. die erste Ableitung hat dort einen Vorzeichenwechsel von + nach -, dann ist der Extremwert ein Maximum.
Ist die zweite Ableitung an der Stelle x* größer als Null, also positiv – bzw. die erste Ableitung hat einen Vorzeichenwechsel von – nach +, dann ist der Extremwert ein Minimum.
Wendepunkte:
Notwendige Bedingung:
Hat die Funktion an der Stelle x* einen Wendepunkt, so ist an der Stelle x* ihre zweite Ableitung gleich Null.
Hinreichende Bedinung:
Ist die dritte Ableitung an der Stelle x* ungleich Null, so hat die ursprüngliche Funktion an der Stelle x* mit Sicherheit einen Wendepunkt.
(In unseren Beispielbildern fehlt das Bild der dritten Ableitung. Sie wäre eine Konstante, also eine Gerade, die oberhalb der x-Achse parallel zur x-Achse verläuft, z.B.: y=1, da die zweite Ableitung in dem Bild eine konstante, positive Steigung hat)